About Vega
The fifth brightest of all stars, and the third brightest in the northern sky. It will be the north polar star in about 12,000 years. In moving through the Milky Way Galaxy, the Sun is generally heading toward the position now occupied by Vega. At a distance of 7.8 parsecs (25.3 light-years, or 2.4 × 1014 km, or 1.49 × 1014 mi), Vega, or α Lyrae, is the prototypical star of spectral class A0V, indicating that it has an effective surface temperature of 9600 K (16,800°F) and derives its energy from the thermonuclear burning of hydrogen in a stable core region.
And so, Vega is really a name of a star.
But surprisingly, Vega affects option values, even when it is 25.3 light-years away. So, we best give it some attention.
Vega is an option model parameter that affects the value of an option, by the indicated amount, when Implied Volatility (IV) changes by 1%.
We will illustrate the concepts surrounding Vega by using Apple(AAPL) options. AAPL currently trades at $150.20
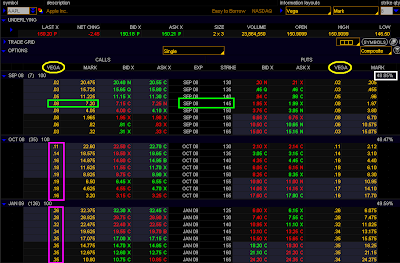
Sept145Call has a value of 7.20, and a vega of 0.08. The IV of this option is ~ 49%. If IV increases by 1% to 50%, this Sept145Call value will become approximately 7.28 (7.20 + 0.08). If the same call option's IV increases by 10%, thus making it 59%, then the Sept145Call will have a value of 8.00, because the vega will have increased by 10 times, from 0.08 to 0.8, as a result of 10% increase in IV.
Therefore, increasing the IV, increases the vega, which in turn increases the values of all options.
Conversely, should AAPL's volatility drop, say by 1% from 49% to 48%, that very same Sept145Call, whose original value was 7.20, now becomes 7.12 (7.20 - 0.08)
Now, you get the macro picture that IV affects option pricing via Vega (and other greeks, like Theta).
Why is Vega important?
It is important because if you were Long an option, whether a Long Call or a Long Put, you want your value of these options to go up. One way, in which these option values can increase, is by having large +ve Vegas. So that in the event, the IV increases, that large +ve Vega will also increase significantly enough to cause your option values to go up.
But, if you had WRITE Calls of Puts, you will want the value of those options you short, to decrease in value (sell high, buy low concept). One way for these options to decrease their values, is to possess -ve Vegas. In fact, when you have a NET Short position, that will automatically generate -ve Vegas.
-ve Vegas can hurt your overall portfolio, if IV spikes.
Note also that vega is smaller in the front months as compared to the further out months. This means that when IV changes, the further out months option values are more impacted because they possess larger Vegas as compared to the nearer months options.
Most traders do not to focus on Vega becos it is arguably more important to know how the IV is behaving. Afterall, what changes the vega is IV. Vega is just a resultant figure.
When IV increases all option values increase (it is so critical that it warrants repetition), for all Calls and Puts. And conversely, when IV drops, all option values drop, both Calls and Puts.
Look at the Theoretical Price (highlighted within green box)of both Calls and Puts when IV is adjusted up by 10%.

They are all higher than the "mark" value, which is the current traded value. You can easily imagine that when the IV drops by 10%, the values of all options, in each strike of each month, and every month, will decrease in value.
There is absolutely no need for AAPL share price to move 1 cent, for IV to cause option value to change drastically. This is the power of IV. So, Asian traders, the next time you buy a Call or Put warrant, remember, don't get suckered by the issuer adjusting the IV upwards. Once you buy, they turn down the IV, and without price changes to your underlying, the warrants can still lose a heck lot of value. Now, you know why warrants offered for trading in asian bourses, are ONE-sided trades, and you ain't the banker.
This is yet another reason, why you should be looking to Long options only when IV is comparatively low and Short options when IV is exceptionally high. Historical Volatility is used as a comparison. However, this is not always to be taken at face value. Some stocks' have increased volatility for extended months to years. On the flip side, some stocks which have low volatility, can remain non volatile for a good number of years as well.
Hence, you should not base your decision to go Long or Short by simply looking at Implied Volatility, although, all astute options traders will know IV of their underlying very well.
So, in summary, Implied Volatility rules...which is why no option trader will survive this game without having a very clear understanding of IV. I tell my friends that my mistress' name is Ivy.
The fifth brightest of all stars, and the third brightest in the northern sky. It will be the north polar star in about 12,000 years. In moving through the Milky Way Galaxy, the Sun is generally heading toward the position now occupied by Vega. At a distance of 7.8 parsecs (25.3 light-years, or 2.4 × 1014 km, or 1.49 × 1014 mi), Vega, or α Lyrae, is the prototypical star of spectral class A0V, indicating that it has an effective surface temperature of 9600 K (16,800°F) and derives its energy from the thermonuclear burning of hydrogen in a stable core region.
And so, Vega is really a name of a star.
But surprisingly, Vega affects option values, even when it is 25.3 light-years away. So, we best give it some attention.
Vega is an option model parameter that affects the value of an option, by the indicated amount, when Implied Volatility (IV) changes by 1%.
We will illustrate the concepts surrounding Vega by using Apple(AAPL) options. AAPL currently trades at $150.20

Sept145Call has a value of 7.20, and a vega of 0.08. The IV of this option is ~ 49%. If IV increases by 1% to 50%, this Sept145Call value will become approximately 7.28 (7.20 + 0.08). If the same call option's IV increases by 10%, thus making it 59%, then the Sept145Call will have a value of 8.00, because the vega will have increased by 10 times, from 0.08 to 0.8, as a result of 10% increase in IV.
Therefore, increasing the IV, increases the vega, which in turn increases the values of all options.
Conversely, should AAPL's volatility drop, say by 1% from 49% to 48%, that very same Sept145Call, whose original value was 7.20, now becomes 7.12 (7.20 - 0.08)
Now, you get the macro picture that IV affects option pricing via Vega (and other greeks, like Theta).
Why is Vega important?
It is important because if you were Long an option, whether a Long Call or a Long Put, you want your value of these options to go up. One way, in which these option values can increase, is by having large +ve Vegas. So that in the event, the IV increases, that large +ve Vega will also increase significantly enough to cause your option values to go up.
But, if you had WRITE Calls of Puts, you will want the value of those options you short, to decrease in value (sell high, buy low concept). One way for these options to decrease their values, is to possess -ve Vegas. In fact, when you have a NET Short position, that will automatically generate -ve Vegas.
-ve Vegas can hurt your overall portfolio, if IV spikes.
Note also that vega is smaller in the front months as compared to the further out months. This means that when IV changes, the further out months option values are more impacted because they possess larger Vegas as compared to the nearer months options.
Most traders do not to focus on Vega becos it is arguably more important to know how the IV is behaving. Afterall, what changes the vega is IV. Vega is just a resultant figure.
When IV increases all option values increase (it is so critical that it warrants repetition), for all Calls and Puts. And conversely, when IV drops, all option values drop, both Calls and Puts.
Look at the Theoretical Price (highlighted within green box)of both Calls and Puts when IV is adjusted up by 10%.

They are all higher than the "mark" value, which is the current traded value. You can easily imagine that when the IV drops by 10%, the values of all options, in each strike of each month, and every month, will decrease in value.
There is absolutely no need for AAPL share price to move 1 cent, for IV to cause option value to change drastically. This is the power of IV. So, Asian traders, the next time you buy a Call or Put warrant, remember, don't get suckered by the issuer adjusting the IV upwards. Once you buy, they turn down the IV, and without price changes to your underlying, the warrants can still lose a heck lot of value. Now, you know why warrants offered for trading in asian bourses, are ONE-sided trades, and you ain't the banker.
This is yet another reason, why you should be looking to Long options only when IV is comparatively low and Short options when IV is exceptionally high. Historical Volatility is used as a comparison. However, this is not always to be taken at face value. Some stocks' have increased volatility for extended months to years. On the flip side, some stocks which have low volatility, can remain non volatile for a good number of years as well.
Hence, you should not base your decision to go Long or Short by simply looking at Implied Volatility, although, all astute options traders will know IV of their underlying very well.
So, in summary, Implied Volatility rules...which is why no option trader will survive this game without having a very clear understanding of IV. I tell my friends that my mistress' name is Ivy.

No comments:
Post a Comment